In mathematics, the sign function or signum function (from signum,Latin for "sign") is an odd mathematical function that extracts the sign of a real number. In mathematical expressions the sign function is often represented as sgn.
Definition:
The signum function of a real number x is defined as follows:
Properties:
Any real number can be expressed as the product of its absolute value and its sign function:
It follows that whenever x is not equal to 0 we have
Similarly, for any real number x,
The signum function is the derivative of the absolute value function (up to the indeterminacy at zero): Note, the resultant power of x is 0, similar to the ordinary derivative of x. The numbers cancel and all we are left with is the sign of x.
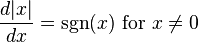
- So basically Signum Function sgn(x) has a domain of any Real Numbers
- and a range of {-1,0,1}.

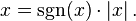
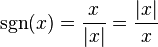
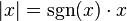
No comments:
Post a Comment