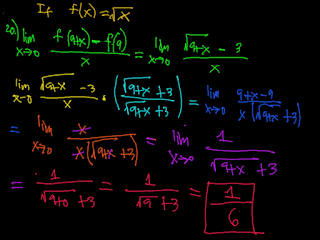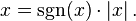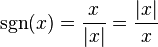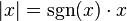Find the derivative by Increment Method(Differential Calculus)

Limits Solution on Love and Rainville Textbook Page 18 No. 29-38

Limits Solution on Love and Rainville Textbook on Page 18 No. 29-38

Limits Examples

Differential Calculus (Graph of y=x|x|)

Graph \[y = x|x|\]

Table of Values:

Graph

Note: Scaling on x and y axis are different.

Graphics are Generated by Wolfram|Alpha.

Differential Calculus(Example 4 of the Graph of Signum Function)

Graph \[y = {x^2}{\mathop{\rm sgn}} (x - 1)\]

Table of Values:

Graph:

Note: Scaling on x and y axis are different.


Thanks to Wolfram|Alpha for the Graphics.

Differential Calculus(Example 3 of the Graph of Signum Function)

Graph \[y = {x^2} + {\mathop{\rm sgn}} (x - 1)\]

This is it's table of values of  from x -5 to 5.

Graph

Note that scaling on x and y axis are different.

Thanks to Wolfram|Alpha for the Graphics.

Differential Calculus (Example 2 of Signum Function Graph)

\[{\rm{Graph}}\] \[y = x - |x|\]

Table of Values

Graph

Differential Calculus(Example 1 of the Graph of Signum Function)

Graph \[y = \frac{1}{2}(1 - {\mathop{\rm sgn}} (x)){x^2}\]

Here's what I get when I make table of values for this:

You should not be confused about the Signum Function sgn(x) because basically it only give
-1,0 and 1. Because it is a sign function, meaning it decides the sign.
If x<0,     sgn(x)=-1
   x=0       sgn(x)=0
   x>0       sgn(x)=1
Those value of sgn(x) are the range that you have to put on sgn(x) depend on the sign of
the x's.

Enjoy Widgets on Our Sites!

Now we have a Partial Fraction Decomposition, Function Grapher, Derivative Solver, Wikipedia, Integral Calculus of Solid of Revolution Solver.

Differential Calculus (What is a Signum Function?)

From: Wikipedia

In mathematics, the sign function or signum function (from signum,Latin for "sign") is an odd mathematical function that extracts the sign of a real number. In mathematical expressions the sign function is often represented as sgn.

Definition: 
The signum function of a real number x is defined as follows:

Properties:

Any real number can be expressed as the product of its absolute value and its sign function:

It follows that whenever x is not equal to 0 we have

Similarly, for any real number x,

The signum function is the derivative of the absolute value function (up to the indeterminacy at zero): Note, the resultant power of x is 0, similar to the ordinary derivative of x. The numbers cancel and all we are left with is the sign of x.

 

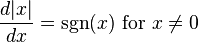
So basically Signum Function sgn(x) has a domain of any Real Numbers 

and a range of {-1,0,1}.

Operation Research I (Cases of Feasible Region base on authors own Conclusion)

Operation Research I (Cases of Feasible Region base on authors own Conclusion).

1. Unbounded Feasible region with minimum optimal solution but no maximum.
2. Unbounded Feasible region with maximum optimal soulution but no minimum solution.

Operation Research I (When will an LP have an unbounded FR?)

Question: When will an LP have an unbounded FR?

Ans: If the feasible set is unbounded, there may or may not be an optimum,
depending on the specifics of the objective function. For example,
if the feasible region is defined by the constraint set {x ≥ 0, y ≥ 0},
then the problem of maximizing x + y has no optimum since any candidate
solution can be improved upon by increasing x or y; yet if the problem
is to minimize x + y, then there is an
optimum (specifically at (x, y) = (0, 0)).
Since it is unbounded, you can continue to find larger and larger solutions.
The fact that the solution space is not restricted means there are endless
possible solutions, many with extremely high values. This means there is no
set optimal solution. There are infinite possibilities which can lead to an
infinite solution.

Operation Research I (What is redundant constraint?)

Question:   What is redundant constraint?

Ans: Redundant constraints are a constraints that don't
    contribute on feasible optimal solution region.
Omitting redundant constraints will not affect
the feasible region.

Operation Research I (When is an LP infeasible?)

Question:         When is an LP infeasible?

Ans:    A linear program is infeasible if there exists
no solution that satisfies all of the constraints
    -- in other words, if no feasible solution can be
    constructed. Since any real operation that you are
    modelling must remain within the constraints of reality,
    infeasibility most often indicates an error of some kind.
   

Operation Research I (When will an LP (Linear Programming) have multiple Solution?)

Question :When will an LP (Linear Programming) have multiple Solution?


Ans: When the feasible region is unbounded.